Advanced optimization

In iterative optimization we attempt to approximate a solution to a problem by making an initial guess and improving this guess over the iterations. In order to improve on such a guess we need a measure of how close our approximation is to the actual optimal solution.

Example

Imagine we were trying to computationally generate the following layout of colors over the grid cells (1-9).

It is a simple problem, because we know exactly how the colors should be laid out to achieve this solution. However, the solution isn’t always this obvious. And so we will try to come to this solution through iterative optimization instead.

Random guess

The first step to solving this algorithmically is to simply choose a random layout of colors.

How good is this random guess? How close is it to the optimal layout? Let’s set up some rules for how correct a layout is, for example:

1. Yellow colors want to be in the top row

2. The purple color wants to be on the bottom row

3. Red colors want to be on the left

4. Green colors want to be on the right

5. The blue color wants to be in the middle

A layout that follows these rules more closely than another layout is a better layout. In order to measure this ’correctness’ we can give scores to a layout. The higher the score the more closely it follows the rules we have set up.

Scoring

If we give 1 point for every grid cell that follows each of the rules we would score our initial guess as such:

1. Yellow colors want to be in the top row (0 out of 3 points)

2. The purple color wants to be on the bottom row (0 out of 1 points)

3. Red colors want to be on the left (1 out of 2 points)

4. Green colors want to be on the right (0 out of 2 points)

5. The blue color wants to be in the middle (0 out of 1 points)

If we add up all these scores that gives our initial guess a total score of 1, pretty bad. Let’s try improving on that.

Iterating

A naive way of improving the layout would be to generate a completely new grid and compute its score again. If the score is higher than the last layout, we will keep this new grid. If the score isn’t higher then we will keep the previous layout.

The longer you let this algorithm generate random layouts the greater the chance that your layout approaches the optimal solution shown in Figure 1. Observe the following progression:

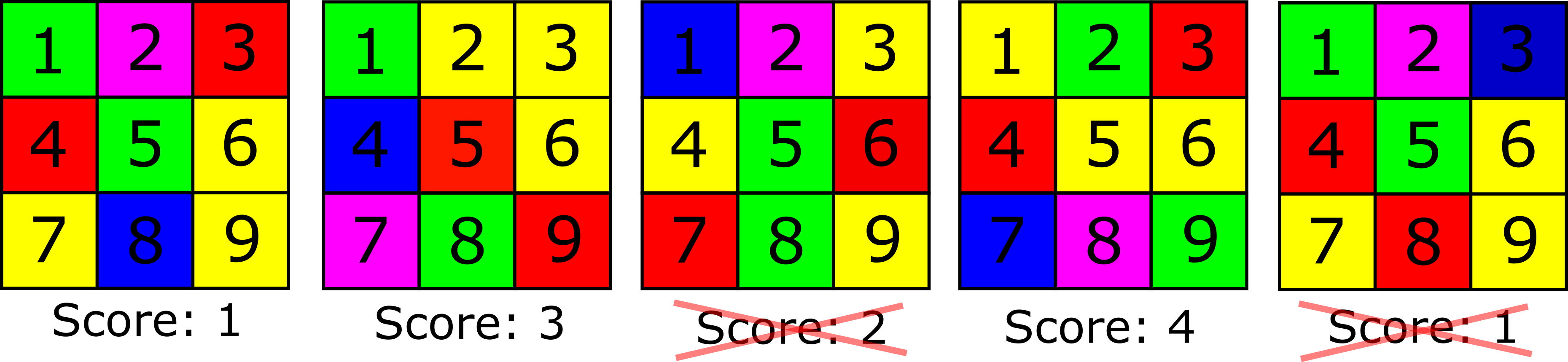
It starts with a random layout with a score of 1, then a new layout is generated that has a score of 3. We keep this new layout, since the score is higher than our previous one. Now we generate another layout, but this time the score is lower than our previous score and so we discard it.

On the next layout we get a score of 4, so this is now our best approximation. The layout after it has a score lower than 4 so again we discard it.

It will obviously take a while for this naive method to converge to the correct solution, and it would need to randomly generate the correct solution by pure chance, and then we would accept it.

Another method

Another naive method that is closer to a smarter solution is that instead of generating a completely random grid every iteration, we swap two tiles in our existing grid.

That is, we randomly pick two locations in the grid and swap their colors. Now we compute whether this new configuration of colors is better than before we swapped those two tiles. If it is, then we keep the tiles as they are now, if it isn’t, then we swap the tiles back to their original position.

A non-naive method

In the last method we randomly swapped some tiles with no regard as to how correct those tiles were. Also we didn’t take into account any history of swapping. As a consequence it might happen that we swap tiles that were in their perfect positions already. We obviously discard such a change as that would impact the score negatively, but essentially it is a wasted iteration.

A smarter way of swapping would be to look at which tiles were producing a low positive impact on the overall score. For if these tiles don’t impact the score very positively, they are probably not in the place they want to be in.

Another improvement would be to keep track of the immediate history of swaps that we have attempted. It makes no sense to swap the same tiles we just attempted to swap on the previous iteration.

There are a lot of clever tricks to think of in order to have less wasted iterations and move towards a solution quicker.